Cálculo integral: 2013

domingo

Integración de funciones trigonometrícas

Seno

Coseno

Tangente

Solución de una integral por partes

Integración por sustitución simple

Cálculo del área bajo una curva por integración

Integral definida y sus propiedades básicas

¿Integral definida e indefinida? ¿ Cuál es la diferencia?

En matemáticas, la integración es la forma de resolver, desde el cálculo integral, dos problemas clásicos del Análisis Matemático, estrechamente relacionados:

El cálculo de áreas y volúmenes de figuras geométricas conocidas.
La obtención de la primitiva de una función, esto es, aquella cuya derivada es la función dada, realizando la "operación inversa" a la derivación.

Los estudios de Isaac Barrow, Isaac Newton y Gottfried Leibniz, dieron forma al teorema fundamental del cálculo, que establece la íntima relación en la solución de ambos problemas. Se denomina integración definida a la obtención del área bajo una curva, e integración indefinida a la operación inversa de la derivación. También se denomina integración a la resolución de una ecuación diferencial, una ecuación en la que la incógnita es una o varias funciones y sus derivadas.

Fuente(s):
http://es.wikipedia.org/wiki/Integral

Introducción al cálculo integral

La idea del cálculo integral consiste en calcular, en general, superficies curvilíneas, es decir, el área entre la gráfica de una función y el eje-x.

Estamos de acuerdo con la siguiente notación:

$\int\limits_a^b f(x)\,\mathrm dx$

Es la integral definida de la función f de [variable] x [los límites] de A a B. Se pretende que la zona entre la curva y los ejes como en la imagen de arriba S. Más específicamente, es que esta es una integral de Riemann (por ejemplo, Riemann), hay también integrante líneas generales.

El cálculo integral se refiere al cálculo de integrales tales.

Aspecto geométrico

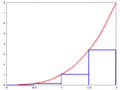
Para hacer la integral de manera sistemática "de vuelta al espacio", que es abordado por las llamadas sumas superior e inferior de rectángulos cada vez más precisos.

segun integral de Riemann
por exceso

Las áreas de los rectángulos ahora se pueden calcular fácilmente, así que tenemos un límite superior y un límite inferior para la zona.

$\int_0^1 x^2\mathrm dx$	$>R_1\,$	$+R_2\,$	$+R_3\,$	$+R_4\,$
	$=\frac14\cdot0^2$	$+\frac14\cdot\left(\frac14\right)^2$	$+\frac14\cdot\left(\frac24\right)^2$	$+\frac14\cdot\left(\frac34\right)^2,\qquad\text{donde cada rectangulo }\tfrac14\text{ largo y tan alto}$
	$= 0{,}21875\,$

Analógamente la suma superior calculada:

$\int_0^1 x^2\mathrm dx$	$<R_1\,$	$+R_2\,$	$+R_3\,$	$+R_4\,$
	$+\frac14\cdot\left(\frac14\right)^2$	$+\frac14\cdot\left(\frac24\right)^2$	$+\frac14\cdot\left(\frac34\right)^2$	$+\frac14\cdot\left(\frac44\right)^2$
	$= 0{,}46875\,$

Entonces vale:

$0{,}21875<\int_0^1 x^2\mathrm dx< 0{,}46875$

Para un enfoque general

Aqui se tiene para la n-esima suma por defecto $U_n$ :

$U_n=\frac1n\cdot0^2+\frac1n\cdot\left(\frac1n\right)^2+\frac1n\left(\frac2n\right)^2+\frac1n\cdot\left(\frac3n\right)^2+\cdots+\frac1n\cdot\left(\frac{n-1}n\right)^2$

y la n-esima suma por exceso $O_n$ :

$O_n=\frac1n\cdot\left(\frac1n\right)^2+\frac1n\left(\frac2n\right)^2+\frac1n\cdot\left(\frac3n\right)^2+\cdots+\frac1n\cdot\left(\frac nn\right)^2$

Y para sacar el valor exacto de la Integral, definimos formalmente

$\int_1^2x^2\mathrm dx=\lim_{n\to\infty}U_n=\lim_{n\to\infty}O_n$

que en el caso es la igual.

Primero sacamos por la suma por exceso:

$\left.O_n=\frac1n\cdot\left(\frac1n\right)^2+\frac1n\left(\frac2n\right)^2+\frac1n\cdot\left(\frac3n\right)^2+\cdots+\frac1n\cdot\left(\frac nn\right)^2\qquad \right|\text{ factorizamos por }\tfrac1n\text{, quadriere die }\mathrm{Br\ddot uche}$

$=\left.\frac1n\left[\frac{1^2}{n^2}+\frac{2^2}{n^2}+\frac{3^2}{n^2}+\cdots\frac{n^2}{n^2}\right]\qquad\qquad\qquad \right|\text{ resolvemos }\tfrac1{n^2}\text{ las potencias}$